任意の周期数列を作るその3

周期 m（奇数）

まずは ${a_n}$ の周期 $m$ が奇数のときです。

周期 $m$ の任意の数列を作るには一次独立な異なる数列が $m$ 個必要ですから、次の規則に従って $m$ 個の数列 $f_m(n,\ 0)$ ～ $f_m(n,\ m-1)$ を作ります。

すると、 $\{a_n\}$ の一般項は係数 $t_1$ ～ $t_m$ を用いて次のように表せます。

$\displaystyle a_n = \sum_{k=1}^{m} {t_kf_m(n,\ k-1)}$

係数 $t_1$ ～ $t_m$ は次の行列で与えられる実数です。

$m$ が奇数のときに上の逆行列が存在することはどうしたら証明できるんでしょうかね･･･

$m=3$ から $m=29$ のときに逆行列を持つことは確認済みです。

$m$ が大きくなるごとに行列式の絶対値が増えていっているので恐らく大丈夫なはずです･･････多分･････････(っ◞‸◟c)

周期 m（偶数）

次に、作りたい数列の周期 $m$ が偶数のときを考えます。

$m$ を $2$ で割りきれるだけ割ったら奇数 $p$ になったとき、適当な自然数 $k$ を用いて $m=2^k \times p$ と書けます。

$p$ は奇数なので、上に書いた通りに $p$ 個の数列 $f_p(n,\ 0)$ ～ $f_p(n,\ p-1)$ を作ると周期 $p$ の任意の周期数列の一般項が作れます。

それを[前回の記事]でやったように、周期を2倍にする操作を $k$ 回行うことによって、周期 $m$ の数列の一般項を作ることができます。

周期 $p$ の任意の周期数列の一般項は $\displaystyle \sum_{i=1}^{p} {t_if_p(n,\ i-1)}$ と表せますが、これに次の操作を $k$ 回施します。

$\displaystyle \operatorname{sgn}\left(\sin{\frac{(2n-1)\pi}{2a}}\right)$ は0にならないので $\displaystyle \frac{\sin{\frac{(2n-1)\pi}{2a}}}{\left|\sin{\frac{(2n-1)\pi}{2a}}\right|}$ とも書けます。前回の記事と同じ処理をしていることになります。

具体的には、 $\displaystyle \sum_{i=1}^{p} {t_if_p(n,\ i-1)}$ は1度目の延長操作で

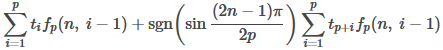
となり、2回目の延長操作で（sgn(～)をf_p(n, k)に含めてΣを結合し、Σの範囲を1から2pとして変換する）

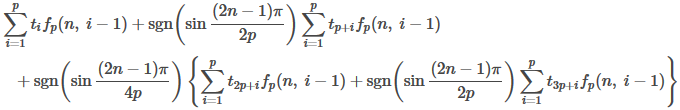
となり、3回目の延長操作で

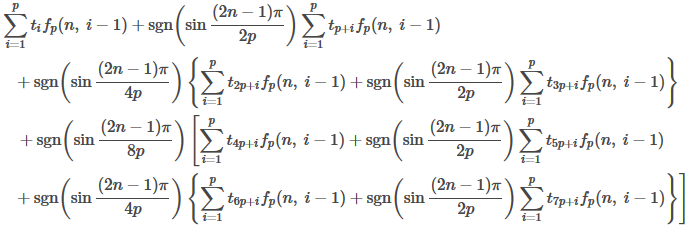
となり、といった感じで2倍2倍2倍2倍･･････に伸ばしていきます。

$k$ 回伸ばしたら周期 $m$ の一般項の原型の出来上がりです！

残る作業は，係数 $t_1$ ～ $t_m$ を求めることのみです。

$m$ が奇数のとき、係数を求めるのにでっかい行列の逆行列を使っていました。

その逆行列を

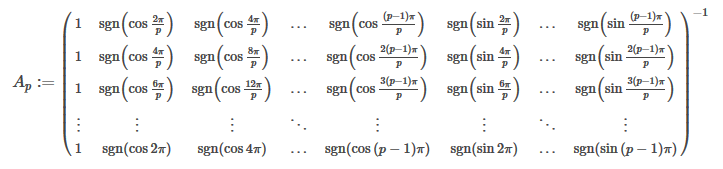
とおきます。そして

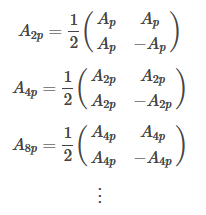
というように行列をさらに $k$ 個作ると、 $A_m = A_{2^k \times p}$ に到達します。

そのとき、一般項の係数 $t_1$ ～ $t_m$ は

${ \left( \begin{array}{c} t_1 \\ t_2 \\ t_3 \\ \vdots \\ t_m \\ \end{array} \right) = A_m \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_m \\ \end{array} \right)}$

で求められます。

書き方や表現が違いますが、今までやってきたことは前回の記事の後ろの方でやったことと同じ原理です。

本質的に異なるところは周期が任意の奇数の数列を作った箇所のみです。

実際に1つ周期数列の一般項を作って、この記事を締めくくりたいと思います。

周期数列 1, 1, 4, 5, 1, 4, 1, 9, 1, 9, 1, 1, 4, 5, 1, 4, 1, 9, 1, 9, ...

ふ･･･深い意味なんてないんだからねっ！///

この数列の周期は $m=10=2^1 \times 5$ です。

まずは①，②，③に従って $5$ つの数列を作ります。

上の5つの数列の一次結合は $\displaystyle \ \sum_{i=1}^{5} {t_if_5(n,\ i-1)}\$ となります。

$5 \times 2^1 = 10$ なので、求める周期数列の一般項は1回の延長操作をして

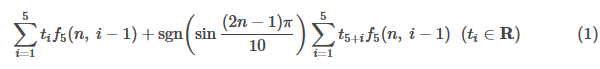
と表せます。

次に係数 $t_i$ を求めます。 $5$ 次正方行列 $A_5$ を

で定めます。

次に、 $10\ (=m)$ 次正方行列 $A_{10}=A_m$ を

で定めます。

この $A_m$ から、係数 $t_i$ が次のように求まります。

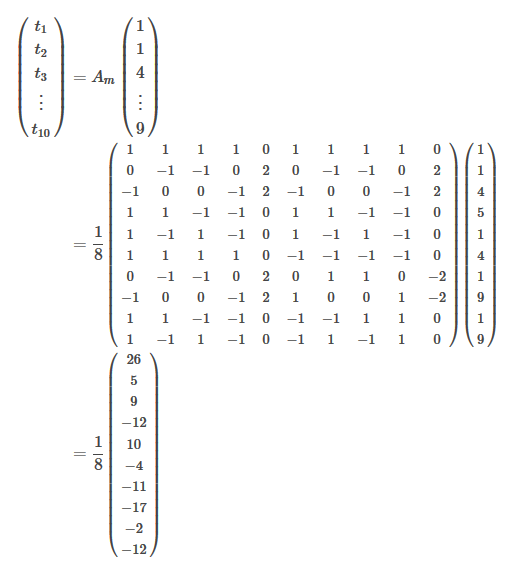
これを $(1)$ 式に代入すれば、求める一般項は

となります！

欠点

この方法の欠点はコンピューターでの浮動小数点計算には向いていていないところ、そしてグラフが連続ではなくﾎﾞｯｺﾎﾞｺで汚いところです。

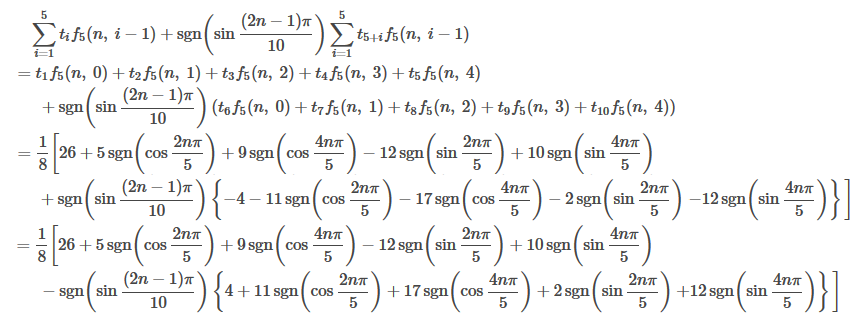
コンピューターで一般項を浮動小数点計算すると本来 $\operatorname{sgn}(0)=0$ となってほしいところが $\operatorname{sgn}(0.00000000000001)=1$ などと評価されてしまうことがあります。これは $n \equiv 0 \pmod{m}$ のときに発生してしまいます。